一、导数
导数(导函数的简称)的定义:设 是函数
是函数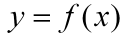 定义域的一点,如果自变量
定义域的一点,如果自变量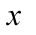 在
在 处有增量
处有增量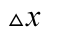 ,则函数值
,则函数值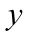 也引起相应的增量
也引起相应的增量 ;比值
;比值 称为函数
称为函数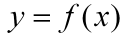 在点
在点 到
到 之间的平均变化率;如果极限
之间的平均变化率;如果极限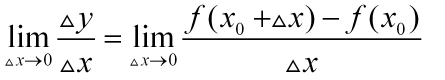 存在,则称函数
存在,则称函数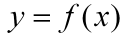 在点
在点 处可导,并把这个极限叫做
处可导,并把这个极限叫做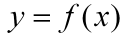 在
在 处的导数,记作
处的导数,记作 或
或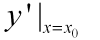 ,即
,即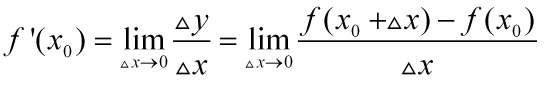 .
.
二、常用导数公式

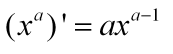



三、求导的四则运算



注:
1、u , v 必须是可导函数
2、若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导。
四、求导与极值

五、曲线梯形面积

六、定积分的定义


七、定积分的几何意义

八、定积分计算

九、定积分的基本性质

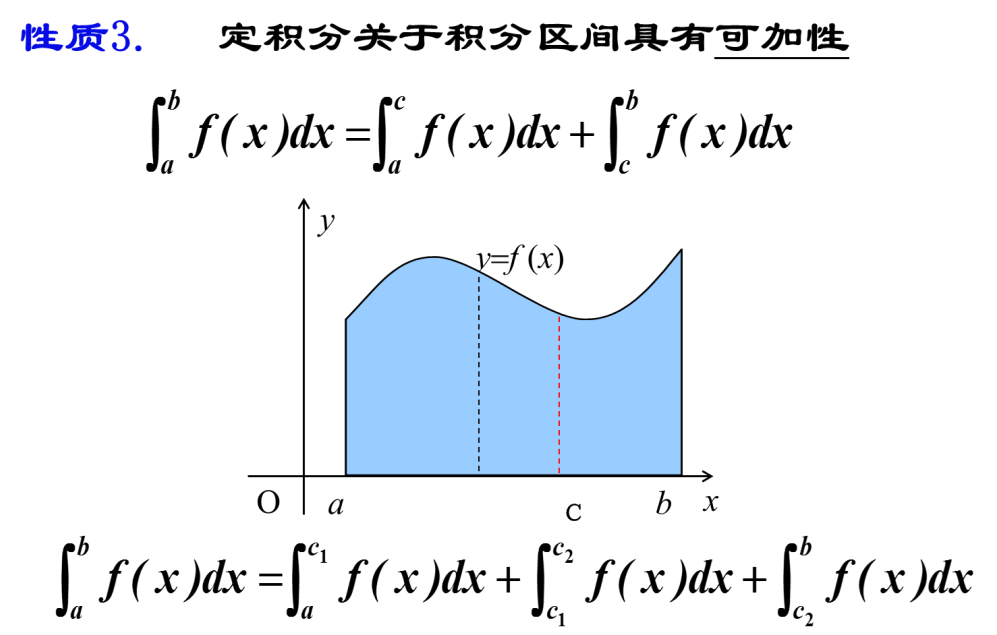
十、分部积分法
